হাটীপতি তাৰকাৰাজ্যৰ অগণন সৌৰজগতৰ ভিতৰত সূৰ্য্যক কেন্দ্ৰ কৰি আমাৰখন অৱস্থিত৷
এইখন সৌৰজগতৰে তৃতীয়টি গ্ৰহ পৃথিৱীত জীৱ সৃষ্টিৰ বহু কোটি বছৰৰ পাছতহে হম’চেপিয়েনচ অৰ্থাৎ ‘মানৱ’ নামৰ প্ৰাণীটোৰ সৃষ্টি হ’ল৷ এই প্ৰাণীটোৰ মস্তিষ্কৰ আচৰিত ক্ষমতাই গ্ৰহটোত আধিপত্য বিস্তাৰ কৰাত সহায় কৰিলে৷
মানৱ মস্তিষ্কই অহৰ্নিশে প্ৰকৃতিৰ সত্য উদ্‌ঘাটনত ব্যস্ত হৈ আছে৷ প্ৰকৃতি অধ্যয়নৰ পৰাই জন্ম হ’ল ‘গণিত’ৰ৷
ভেড়া ৰখীয়াসকলে ভেড়াৰ হিচাপ ৰাখিবলৈ, নীল নদীৰ বানপানীয়ে অনিষ্ট কৰা মাটিৰ পৰিমাণ নিৰ্ণয় কৰিবলৈ, ৰজা-মহাৰজাৰ সমাধি অথবা পিৰামডি বনাবলৈ, প্ৰেমৰ চানেকি তাজমহল বনোৱাৰ পৰা বৰ্তমানৰ উচ্ছতম বিল্ডিং ‘বুৰ্জ খালিফা’ আৰু উচ্ছতম স্মৃতিসৌধ নিৰ্মাণ আদি সকলোতে গাণিতিক তত্ত্বক ব্যৱহাৰ কৰা হৈছে৷
এই গাণিতিক কৌশল ব্যৱহাৰ কৰিয়েই আজিৰ পৰা এশ বছৰৰ আগতে ১৯১৬ চনত বিজ্ঞানী এলবাৰ্ট আইনষ্টাইনে মহাকৰ্ষণীয় তৰংগৰ তত্ত্ব আগবঢ়াইছিল৷
গণিত সৰ্বত্ৰে ব্যাপ্ত৷ দৈনন্দিন জীৱনৰ কোনটো কাম গণিত অবিহনে হ’ব পাৰে আপুনি ভাবকচোন?
জীৱন বাটৰ চকা স্বৰূপ গণিতক কিন্তু বিষয় হিচাপে সকলোৱে ভয় কৰে অথবা বহুতে গণিতৰ পৰা দূৰত্ব বজাই ৰাখিব বিচাৰে৷ কাৰণ আমাৰ সমাজ ব্যৱস্থাতগণিতৰ ওপৰত এক ভ্ৰান্ত ধাৰণা এতিয়াও বৰ্তি আছে৷ সেইবাবে সকলোতে ব্যাপ্ত, সকলোৰে জীৱন বাটৰ সংগী হ’লেও গণিতৰ নাম শুনিলেই সৰ্বসাধাৰণৰ অন্তৰত এক কম্পনৰ সৃষ্টি হয়৷
এই গণিত-ভীতিৰ প্ৰকৃত কাৰণ হ’ল গণিতৰ নান্দনিকতাক সমাজ জীৱনত পৰিচয় কৰাই দিয়াত গুৰু সমাজৰ ব্যৰ্থতা৷
সাহিত্য বিষয়ৰ শিক্ষক এজনৰ লগত শিক্ষাৰ্থীয়ে সহজভাৱে ভাৱ-বিনিময় কৰে, কিন্তু আজিৰ তাৰিখতো বহুতে অংকৰ শিক্ষকজনৰ কাষ চাপিব নিবিচাৰে৷
ছাত্ৰ-ছাত্ৰীৰ মনত বিষয়টোৰ প্ৰতি সৃষ্টি কৰা ভয়ৰ মূল কাৰণটোৱেই হ’ল শিক্ষাগুৰু৷
পাঠদানৰ সময়ত শিক্ষকজন উপপাদ্য, সূত্ৰ, নেওঁতা, পূৰণ, হৰণ, যোগ, বিয়োগ, লেখ আদি সমাধান কৰাতেই লাগি থাকিলে, শিশুসকলৰ মনটো অংকৰ ‘ড্ৰাকুলা’ৰ জগতলে গতি কৰে৷ এই জগতখনত শিক্ষকজনে ড্ৰাকুলা হৈ শিশুসকলক সূত্ৰ, নেওঁতা মুখস্থ ধৰে আৰু নোৱাৰিলে শাস্তি প্ৰদান কৰে৷ শিশুকালতে গঢ় লোৱা গণিত বিষয়ৰ ওপৰত এই মানসিকতা, মৃত্যু পৰ্যন্ত থকা দেখা যায়৷
তাৰে মাজতে এনেকুৱা শিক্ষকো আছে যি গণিতৰ জগতখনক দৈনন্দিন জীৱনৰ লগত সংগতি ৰাখি অধ্যয়নৰ বিষয় কৰি লয়þ৷
বিভিন্ন খেল-ধেমালিৰ মাধ্যমৰে, আৰ্হি প্ৰস্তুতৰ মাধ্যমৰে, হাতে কামে লাগি শিশুসকলৰ বাবে প্ৰয়োজনীয় সকলো সূত্ৰ, উপপাদ্য, সমাধান আদি কৰি দেখুৱায়৷ এনেধৰণে শিক্ষা লোৱা শিশুসকলেই ভৱিষ্যতে প্ৰকৃতিৰ বুকুত থকা গণিতৰ বিভিন্ন ৰহস্য উদঘাটন কৰিবলৈ সক্ষম হোৱাৰ লগতে সমাজক গণিত-ভীতিৰ পৰা মুক্ত কৰিবলৈ আগবাঢ়ি অহা দেখা যায়৷
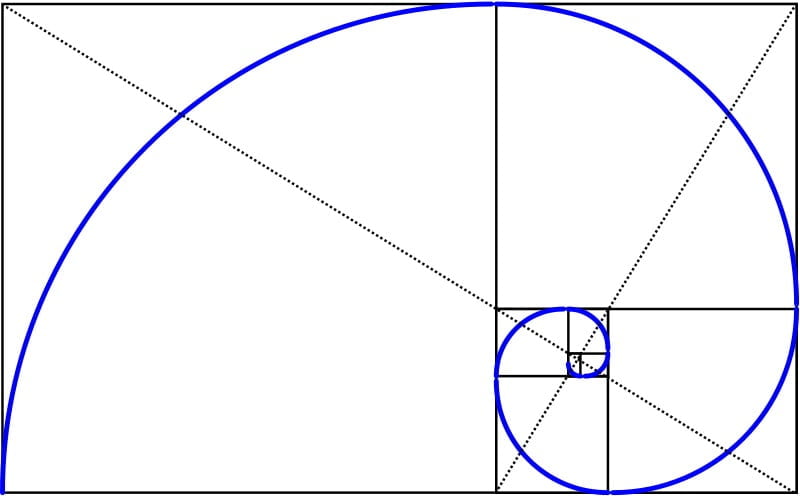
উপৰোক্ত নগণ্য সংখ্যক শিক্ষাগুৰুৰ বাবেই গণিত হৈ পৰে আনন্দৰ বিষয়, যাৰ জৰিয়তে আমি বিশ্বব্ৰহ্মাণ্ডৰ সকলো ৰহস্য ভেদ কৰি থাকিব পাৰিছোঁ৷ গণিতক প্ৰকৃতিৰ লগত জড়িত কৰাৰ চিন্তাৰ ফলতে আমি উলিয়াব পাৰিলোঁ গণিতৰ নান্দনিকতাৰ উৎকৃষ্টতম প্ৰমাণ–সোণালী অনুপাত৷
প্ৰাচীন ইজিপ্তবাসীয়ে আৱিষ্কাৰ কৰিছিল যে, বিভিন্ন প্ৰাকৃতিক বস্তু দেখিবলৈ সুন্দৰ হোৱাৰ কাৰণ হ’ল সেইবোৰত নিহিত হৈ থকা এটা সাংখ্যিক অনুপাত৷ আমি জানো যে, গ্ৰীকতে প্ৰথমে জ্যামিতিৰ আবিৰ্ভাৱ হৈছিল৷ প্ৰাচীন গ্ৰীকৰ গণিতজ্ঞসকলে জ্যামিতিৰ বিষয়ে অধ্যয়ন কৰি থাকোতে প্ৰায়ে ইজিপ্তসকলে আৱিষ্কাৰ কৰা সৌন্দৰ্য্য নিহিত সাংখ্যিক অনুপাতৰ সন্মুখীন হৈছিল৷ তেতিয়াৰ পৰা গ্ৰীকৰ গণিতজ্ঞসকলে এই সাংখ্যিক অনুপাতৰ ওপৰত বিশদভাৱে অধ্যয়ন কৰিব আৰম্ভ কৰিছিল৷
এই সাংখ্যিক অনুপাতৰ প্ৰথম লিখিত সংজ্ঞা ইউক্লিডৰ এলিমেণ্টছ[Elements] নামৰ কিতাপখনত পোৱা গৈছিল৷
প্ৰাচীন যুগৰ পাইথাগোৰাছ আৰু ইউক্লিডৰ সময়ৰ পৰা মধ্যযুগৰ ইটালীৰ গণিতজ্ঞ লিঅ’নাৰ্ড’ অৱ্‌ পিছা [Leonardo of Pisa], জ্যোতিৰ্বিজ্ঞানী জোহান্‌ছ কেপলাৰৰ [Johannes Kepler] পৰা বৰ্তমান যুগৰ অক্সফ’ৰ্ড বিশ্ববিদ্যালয়ৰ পদাৰ্থবিজ্ঞানী ৰ’জাৰ পেনৰ’জে [Roger Penrose] নিজৰ জীৱনৰ বহু মূল্যবান সময় এই সাংখ্যিক অনুপাতৰ ধৰ্মৰ ওপৰত অধ্যয়ন কৰিছিল৷
এই সাংখ্যিক অনুপাতক বৰ্তমান ‘সোণালী অনুপাত’ নামেৰে জনাজাত৷
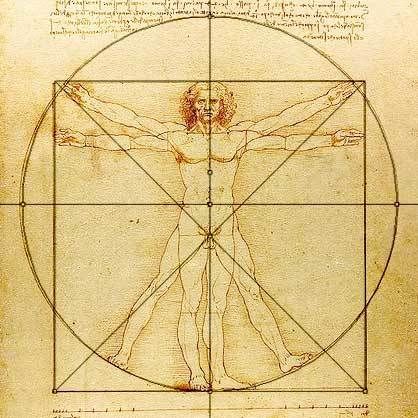
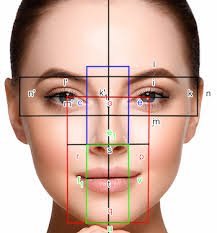
সোণালী অনুপাত কেৱল গণিতজ্ঞসকলৰ কাৰণেই যে প্ৰয়োজন তেনে নহয়; জীৱবিজ্ঞানী, শিল্পী, সংগীতিজ্ঞ, বুৰঞ্জীবিদ, ভূতত্ত্ববিদ, দাৰ্শনিক, স্থাপত্যবিদৰ লগতে সিদ্ধযোগীসকলেও সোণালী অনুপাতক এৰাই চলিব নোৱাৰে৷ কাৰণ গোটেই প্ৰকৃতিৰ সৃষ্টিতে সোণালী অনুপাত নিহিত হৈ আছে৷ মহাকাশত থকা সৰ্পিল তাৰকাৰাজ্যসমূহৰ পৰা বিভিন্ন স্ফটিক, তৰামাছ, গছৰ পাত, ফুল, শামুকৰ খোলা, জন্তুৰ পাকখোৱা শিং, পখিলা, মানুহৰ শৰীৰটোৰ প্ৰতিটো অংগ, চৰাইৰ কণীটোৰ পৰা ধৰি মনালিছাৰ ফটোখনলৈকে সকলোতে এই অনুপাত সোমায় আছে৷
স্থপতিবিদসকলে এই অনুপাত ব্যৱহাৰ কৰি পিৰামিড, দা গ্ৰেট ৱাল অৱ চাইনা, তাজমহলৰ পৰা বৰ্তমানৰ বুৰ্জ খলিফালৈকে নক্সা প্ৰস্তুত কৰি নিৰ্মাণ কৰিছিল৷ সোণালী অনুপাত সোমাই থকা সৰ্পিল সৌৰজগতৰ গঠনৰ আৰ্হিৰে কেইবামহলীয়া ঘৰৰ ভূমিকম্প-প্ৰতিৰোধী চিৰি নিৰ্মাণ কৰাটো বৰ্তমান যুগৰ উল্লেখনীয় সাফল্য৷
চিত্ৰশিল্পীয়ে মনালিছাৰ ফটোখন আঁকোতে, গাড়ীৰ ডিজাইনাৰসকলে সকলোকে মোহিত কৰিব পৰা গাড়ী এখন প্ৰস্তুত কৰোতে, সোণালী অনুপাত ব্যৱহাৰ কৰি আহিছে৷ আনকি সাধাৰণ কাঠমিস্ত্ৰী এজনে বনোৱা দৰ্জা, খিৰিকী, ভেণ্টিলেচন, টেবুল, চকীতো ক’ব নোৱাৰাকৈ সোণালী অনুপাত ব্যৱহাৰ হয়৷
আমি কেতিয়াও সম্পূৰ্ণ ‘বৰ্গাকাৰ টেবুল’ মিস্ত্ৰীয়ে বনোৱা নেদেখো৷ মিস্ত্ৰীক সুধিলে ক’ব, ‘‘দেখিবলৈ বেয়া লাগিব’’৷ অৰ্থাৎ দেখিবলৈ ভাল লগা সকলোতে ‘সোণালী অনুপাত’ নিহিত হৈ আছে৷ এই অনুপাতৰ কম বেছি পৰিমাণে দেখাত শুৱনী অথবা কুৎসিতৰ বিশেষণ দিয়ে৷
এতিয়া কথা হ’ল এই সোণালী অনুপাতনো [Golden Ratio] কি ?
সাণালী অনুপাতৰ বিশদ বৰ্ণনা ১৫০৯ চনত প্ৰকাশ হোৱা লুকা পাকিওলিৰ [Luca Pacioli] কিতাপ ডি ডিভাইনা প্ৰ’প’ৰশ্বনিত [De divina proportione] উল্লেখ আছে৷
এলিমেণ্টছ কিতাপখনত উল্লেখ থকা তথ্য অনুসৰি, সোণালী অনুপাতৰ সংজ্ঞা এনেধৰণৰ– এডাল সৰল ৰেখাক যদি এনেদৰে ভাগ কৰা হয় যে, ইয়াৰ চুটি অংশ আৰু দীঘল অংশৰ অনুপাত; দীঘল অংশ আৰু গোটেই ৰেখাডালৰ অনুপাতৰ সৈতে সমান হয়, তেন্তে সেয়ে হ’ব সোণালী অনুপাত৷
ইউক্লিডে তেখেতৰ ‘এলিমেণ্টছ’ নামৰ বিখ্যাত কিতাপখনত সোণালী অনুপাতৰ বিষয়ে এডাল সৰল ৰেখা কাটি ব্যাখ্যা কৰিছিল৷ ১৫৯৭ চনত টুবিনগেন [Tubingen] বিশ্ববিদ্যালয়ৰ মাইকেল মেছটিনে [Michael Maestlin] সোণালী অনুপাতৰ এক আনুমানিক অনুপাত প্ৰকাশ কৰে৷
সোণালী অনুপাতৰ মান প্ৰায়8:13 বা 1:1.6180340৷
বিংশ শতিকাৰ পৰা সোণালী অনুপাতক গ্ৰীক্‌ আখৰ ‘ফাই’ৰে বুজোৱাত ব্যৱহাৰ কৰা হয়৷ গণিতজ্ঞ মাৰ্ক বাৰে [Mark Barr], গ্ৰীক্‌ ভাস্কৰৰ্য্যশিল্পী ফিডিয়াছৰ [Phidias] নামত ফাইৰ [Phi] চিহ্নৰে সোণালী অনুপাতক বুজাইছিল৷ সৰুফলাৰ ফাইৰে [j] সোণালী অনুপাত আৰু বৰফলাৰ ফাইৰে [ন্দ্ৰ] সোণালী অনুপাতৰ প্ৰতিক্ৰম বা অনোন্যকক বুজোৱা হয়৷

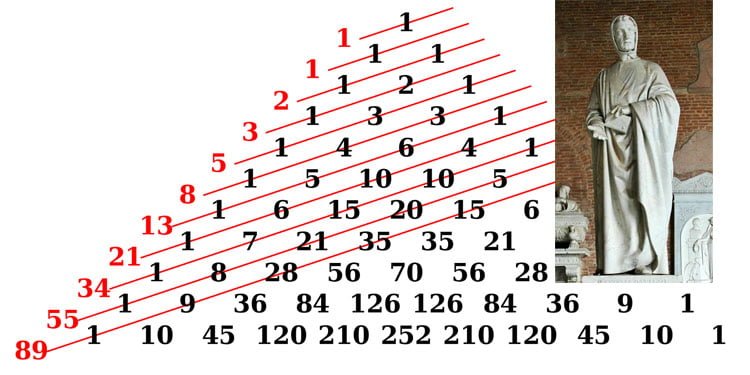
ফিব’নাচ্ছি সংখ্যা [Fibonacci number]
১২০২ চনত ফিব’নাচি সংখ্যাৰ ক্ৰম আৱিষ্কাৰ কৰিছিল ইটালীৰ বিখ্যাত গণিতজ্ঞ লিঅ’নাৰ্ড’ পিছানো [Leonardo Pisano]৷ তেখেত সৰ্বসাধাৰণৰ মাজত ফিব’নাচ্ছি নামেৰে জনাজাত আছিল৷
লিঅ’নাৰ্ড’ৰ গণিতৰ ওপৰত লিখা গুৰুত্বপূৰ্ণ কিতাপখনৰ নাম আছিল ‘লিবাৰ এবাকি’ [Liber abaci]৷
এই আচৰিত ধৰণৰ সংখ্যাৰ ক্ৰম, প্ৰকৃতিৰ প্ৰায় সকলো ক্ষেত্ৰতে দেখা যায়৷ গণিতজ্ঞসকলৰ লগতে উদ্ভিদ বিজ্ঞানী, প্ৰাণী বিজ্ঞানী, স্থাপত্যবিদ, চিত্ৰশিল্পী সকলে শতিকা জুৰি প্ৰকৃতিত থকা এই আচৰিত সংখ্যাৰ ক্ৰমক লৈ ব্যস্ত হৈ পৰিছিল৷ ফুলৰ পাহি, গছ-লতাৰ ডাল-পাতৰ পৰা প্ৰকৃতিৰ প্ৰায় সকলোতে তেখেতসকলে এই সংখ্যা আৱিষ্কাৰ কৰি উৎফুল্লিত হৈ পৰিছিল৷ প্ৰকৃততে ফিব’নাচ্ছি সংখ্যা হ’ল; এটা অসীম অনুক্ৰম, যাৰ ক্ৰমিক সংখ্যাবোৰ তাৰ আগৰ সংখ্যা দুটাৰ যোগফলৰে গঠিত সংখ্যাৰ অনুক্ৰম বোলা হয়৷ গাণিতিক দৃষ্টিকোণৰপৰা এই সংখ্যা শ্ৰেণীটোৰ কেইবাটাও উল্লেখনীয় আৰু আকৰ্ষণীয় ধৰ্ম আছে৷
তলত উল্লেখিত শ্ৰেণীটোৰ তৃতীয় পদৰ পৰা আৰম্ভ কৰি প্ৰতিটো পদ আগৰ পদ দুটাৰ যোগফলৰ সমান৷ আন এটা হ’ল, দুটা বৃহৎ ক্ৰমিক পদৰ অনুপাতৰ মান প্ৰায় 1.618৷
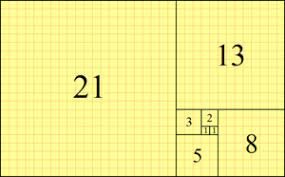
উদাহৰণস্বৰূপে ২৩৩/১৪৪- ১.৬১৮০৫, ৩৭৭/২৩৩ – ১.৬১৮০২, ইত্যাদি৷ যেনে– ১ , ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫ আদি৷
তলত দিয়া সংখ্যাৰ ক্ৰমসমূহ মন দি চাওক–
০ ১ ১ ২ ৩ ৫ ৮ ১৩ ২১ ৩৪ ৫৫ ৮৯ ১৪৪
উপৰোক্ত ক্ৰমসমূহ তাৰ আগৰ সংখ্যা দুটাৰ যোগফলৰে গঠিত হোৱাৰ প্ৰমাণ আমি তলত দিয়া ধৰণে পাম –
0+1=1 1+1=2 1+2=3 2+3=5
3+5=8 5+8=13 8+13=21 13+21=34
21+34=55 34+55=89 55+89=144 89+144=233 আদি৷
প্ৰকৃতিৰ আটাইতকৈ সুন্দৰ সৃষ্টি, বিভিন্ন ফুলৰ পাহিসমূহৰ পৰা আমি সুন্দৰকৈ ফিব’নাচ্ছিসংখ্যাৰ ওপৰত এটি সম্যক ধাৰণা ল’ব পাৰোঁ৷
আমাৰ সকলোৰে পৰিচিত ডেইজী ফুলৰ পাহিবোৰো ক্ৰমে ৩৪, ৫৫ আৰু ৮৯ টা হিচাপে সুন্দৰকৈ সজ্জিত হৈ থাকে৷
ঠিক সেইদৰে ট্ৰেডেছকাণ্টিয়াৰ পাহি ৩ টা, ৱাটাৰকাপ ফুলৰ পাহি ৫ টা , কছমছ ফুলৰ পাহি ১৮ টা, এষ্টাৰ ফুলৰ পাহি ২১ টা, মেৰিগ’ল্ড ফুলৰ পাহি ১৩ টা থাকে৷
চাৰিটা, ছয়টা, সাতটা, চৈধ্যটা আদি পাহি থকা ফুল নাই বুলিয়েই ক’ব পাৰি৷ আচৰিত ধৰণে ফিব’নাচ্ছিৰ সংখ্যাৰ শ্ৰেণীটো এই 4, 6, 7, 14 আদি পোৱা নাযায়৷
ঠিকসেইদৰে এজোপা গছৰ ডালসমূহতো ফিব’নাচ্ছি শ্ৰেণী পোৱা যায়৷ ইয়াৰ পৰাই প্ৰমাণিত হয় যে, সমস্ত সৃষ্টিৰাজিৰ শৃংখলিত ৰূপৰ অন্তৰালত গাণিতিক সূত্ৰ নিহিত হৈ আছে৷
ফ্ৰেক্‌টেল [Fractals]
গণিতৰ জগতৰ আন এক আ(ৰ্য হ’ল– ফ্ৰেক্‌টেল সমূহ৷ ফ্ৰেক্‌টেল শব্দটো ১৯৭৫ চনত পোনপ্ৰথমবাৰৰ বাবে গণিতজ্ঞ বেন’ইট মেণ্ডেলব্ৰট [Benoতব্ধ Mandelbrot] ব্যৱহাৰ কৰিছিল৷
মেণ্ডেলব্ৰটে, ফ্ৰেকটেল শব্দটো লেটিন শব্দ ফ্ৰেকটাছৰ পৰা আনিছে৷
ফ্ৰেকটাছৰ অৰ্থ হ’ল– খণ্ড খণ্ড৷
অনিয়মিত জ্যামিতিৰ প্ৰতি প্ৰকৃতিৰ পক্ষপাতিত্বৰ কথা আলোচনা কৰি তেওঁ এবাৰ কৈছিল, ‘‘ডাৱৰবোৰ গোলক নহয়, পাহাৰবোৰো শংকু নহয়৷’’
যি কি নহওক, মেণ্ডেলব্ৰট নিজেই প্ৰকৃতিৰ জটিল আকৃতিবোৰৰ মাজত শৃংখলা আৰু সমমিতিৰ সন্ধান কৰোঁতাসকলৰ পথ-প্ৰদৰ্শক৷ প্ৰকৃতিয়ে স্বতঃস্ফূৰ্তভাৱে সৃষ্টি কৰা বেছিভাগ জ্যামিতীয় আকৃতি, বিভিন্ন মাপ বা আকাৰ সাপেক্ষে স্ব-সামঞ্জস্য হয়৷
অৰ্থাৎ কোনো বস্তুৰ একোটা অংশৰ অবয়ৱ গোটেই আকৃতিটোৰ সামগ্ৰিক অবয়ৱৰ দৰে একে হয়৷ কিন্তু এনে ক্ষেত্ৰত প্ৰাকৃতিক আকৃতিবোৰৰ কোনো অন্তৰ্নিহিত দৈৰ্ঘ্য-মাপ নাথাকে, যিকোনো পৰ্য্যায়ৰ বিৱৰ্ধনবা বিস্তাৰতে সেইবোৰ দেখিবলৈ একে হয়৷
আমি ফ্ৰেক্‌টেলৰ বিষয়ে সাধাৰণভাৱে বুজিবলৈ হ’লে, এপাহ ফুল কবিক উদাহৰণ হিচাবে ল’ব পাৰো৷ ফুল কবিৰ ডাঙৰ পাহৰ লগত সকলোবোৰ সৰু পাহৰ নক্সা একে হয়৷ যিমানে ক্ষুদ্ৰ টুকুৰা নহওক, ফুলকবিৰ টুকুৰাৰ নক্সা একে থাকে৷
গণিতৰ সমমিতি অধ্যয়ন কৰিবৰ বাবেও বেনইট মেণ্ডেলব্ৰটে ফ্ৰেক্‌টেল ব্যৱহাৰ কৰিছিল৷ প্ৰকৃতিৰ সকলোতে ফুলকবিৰ দৰে ব্ৰক’লি, ঢেকীয়া পাত, গছ, ফুল, ডাৱৰ, পৰ্বত, নদ আৰু উপনদী, বৰফৰ কণা আদিত ফ্ৰেকটেল দেখা পাওঁ৷
ফ্ৰেক্‌টেল আমি কাগজত কাটি কাটি বনাবওঁ পাৰোঁ৷
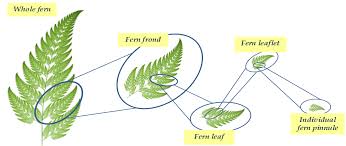
ঢেঁকীয়াজাতীয় উদ্ভিদ প্ৰাকৃতিক ফ্ৰেক্‌টেলৰ সুন্দৰ উদাহৰণ৷ এনে উদ্ভিদৰ এটা ডাল ল’লে দেখা যাব যে ইয়াৰ আকৃতি এটা শাখা ডালৰ অনুৰূপ৷ এটা একেবাৰে সৰু ডালৰ টুকুৰাও ডাঙৰ ডালৰ অনুৰূপ হয়৷
ইয়াকে স্ব-সমঞ্জস্য বোলা হয়৷
মানুহৰ হৃদযন্ত্ৰৰ প্ৰতিটো অংশই ফ্ৰেক্‌টেলৰ এক সুন্দৰ উদাহৰণ৷
প্ৰকৃতিৰ সকলো বস্তুৱেই কিছুমান আকাৰ-আকৃতিৰে নিৰ্দিষ্ট দীঘ-মাপৰে গঠিত বুলি আমি সোণালী অনুপাত, ফিব’নাচ্ছিৰ শ্ৰেণী আৰু ফ্ৰেক্‌টেলৰ লিখনিৰ পৰা গম পাইছো৷
মানুহৰ শৰীৰৰ উচ্ছতা, তাৰ হাড়বোৰৰ দৃঢ়তাৰ লগতে মধ্যাকৰ্ষণিক বলৰ লগত পোনপটীয়া সম্পৰ্ক আছে৷
ঠিক সেইদৰে চৰাই এটা কিমান ডাঙৰ হ’ব পাৰিব, সেইটো নিৰ্ভৰ কৰিব সিহঁতৰ ডেউকা আৰু বুকুৰ মাংসপেশীৰ শক্তিৰ ওপৰত৷
এনেকুৱা আৰু অসংখ্য গাণিতিক বিস্ময় প্ৰকৃতিৰ বুকুত অন্তৰ্নিহিত হৈ আছে৷ ইয়াৰে কিছুমানৰ বিষয়ে বৰ্তমানলৈকে আমি জ্ঞান অৰ্জন কৰিব পৰাগৈ নাই৷
ভাবিলে আচৰিত লাগে পৃথিৱীত থকা জীৱৰ পৰা বিশ্বব্ৰহ্মাণ্ডৰ নক্ষত্ৰপুঞ্জলৈকে সকলোতে এই সূত্ৰ কেনেকৈ নিহিত হৈ আছে!
[বিজ্ঞান জেউতি, অক্টোবৰ-নৱেম্বৰ, ২০১৭]